How Do You Know Where the 60 Degree Angle Is in a Triangle
Acute, obtuse, isosceles, equilateral…When it comes to triangles, there are many different varieties, but only a pick few that are "special." These special triangles have sides and angles which are consistent and predictable and can be used to shortcut your mode through your geometry or trigonometry problems. And a 30-60-ninety triangle—pronounced "30 60 90"—happens to be a very special blazon of triangle indeed. In this guide, we'll walk yous through what a thirty-lx-90 triangle is, why it works, and when (and how) to apply your knowledge of it. So permit'due south get to it! A thirty-threescore-xc triangle is a special right triangle (a right triangle existence whatever triangle that contains a 90 degree bending) that e'er has degree angles of 30 degrees, 60 degrees, and ninety degrees. Because it is a special triangle, information technology also has side length values which are always in a consistent human relationship with one another. The basic 30-60-ninety triangle ratio is: Side reverse the 30° angle: $ten$ Side reverse the 60° angle: $ten * √three$ Side opposite the 90° angle: $2x$ For example, a 30-60-90 degree triangle could take side lengths of: 2, 2√3, 4 7, 7√iii, xiv √3, 3, 2√3 (Why is the longer leg three? In this triangle, the shortest leg ($x$) is $√3$, so for the longer leg, $x√three = √3 * √3 = √nine = 3$. And the hypotenuse is 2 times the shortest leg, or $2√3$) And so on. The side contrary the 30° angle is always the smallest, because xxx degrees is the smallest angle. The side opposite the threescore° angle will be the middle length, because 60 degrees is the mid-sized degree angle in this triangle. And, finally, the side contrary the xc° bending will always exist the largest side (the hypotenuse) because xc degrees is the largest bending. Though information technology may look similar to other types of correct triangles, the reason a 30-60-90 triangle is so special is that you merely need three pieces of data in order to discover every other measurement. So long as you know the value of ii bending measures and ane side length (doesn't matter which side), yous know everything y'all need to know most your triangle. For example, nosotros can employ the 30-60-xc triangle formula to fill in all the remaining data blanks of the triangles beneath. We tin can run into that this is a right triangle in which the hypotenuse is twice the length of ane of the legs. This means this must be a thirty-sixty-90 triangle and the smaller given side is opposite the 30°. The longer leg must, therefore, be opposite the 60° bending and measure $6 * √3$, or $six√3$. Nosotros tin can see that this must be a 30-threescore-90 triangle because we can see that this is a right triangle with one given measurement, 30°. The unmarked bending must then be sixty°. Since 18 is the measure contrary the 60° angle, it must be equal to $x√3$. The shortest leg must then mensurate $eighteen/√3$. (Note that the leg length will actually be $xviii/{√3} * {√iii}/{√three} = {eighteen√3}/3 = six√3$ because a denominator cannot contain a radical/square root). And the hypotenuse will be $2(xviii/√iii)$ (Note that, over again, you lot cannot have a radical in the denominator, and so the final answer will actually be 2 times the leg length of $6√3$ => $12√3$). Again, nosotros are given two angle measurements (90° and 60°), and so the 3rd measure will be 30°. Because this is a 30-60-90 triangle and the hypotenuse is 30, the shortest leg will equal xv and the longer leg will equal 15√3. No need to consult the magic eight ball—these rules always work. But why does this special triangle work the fashion it does? How exercise we know these rules are legit? Let'southward walk through exactly how the 30-60-90 triangle theorem works and prove why these side lengths will e'er be consistent. First, allow'southward forget about right triangles for a second and expect at an equilateral triangle. An equilateral triangle is a triangle that has all equal sides and all equal angles. Because a triangle's interior angles always add together upwards to 180° and $180/iii = lx$, an equilateral triangle will always take three sixty° angles. Now let's drop downward a meridian from the topmost angle to the base of the triangle. We've now created two right angles and 2 congruent (equal) triangles. How exercise we know they're equal triangles? Considering nosotros dropped a summit from an equilateral triangle, nosotros've split the base exactly in one-half. The new triangles too share one side length (the elevation), and they each have the aforementioned hypotenuse length. Considering they share iii side lengths in common (SSS), this means the triangles are congruent. Note: not only are the two triangles coinciding based on the principles of side-side-side lengths, or SSS, just as well based on side-angle-side measures (SAS), angle-bending-side (AAS), and angle-side-angle (ASA). Basically? They're most definitely congruent. Now that we've proven the congruencies of the two new triangles, we tin see that the superlative angles must each be equal to 30 degrees (because each triangle already has angles of 90° and sixty° and must add upwards to 180°). This ways nosotros accept made two thirty-60-90 triangles. And because we know that we cut the base of operations of the equilateral triangle in one-half, nosotros tin meet that the side opposite the 30° angle (the shortest side) of each of our thirty-60-90 triangles is exactly half the length of the hypotenuse. And so let us call our original side length $x$ and our bisected length $ten/2$. Now all that leaves u.s.a. to do is to find our mid-side length that the two triangles share. To do this, nosotros tin only utilize the Pythagorean theorem. $a^2 + b^ii = c^ii$ $(ten/two)^2 + b^ii = ten^2$ $b^2 = x^2 - ({10^2}/4)$ $b^2 = {4x^ii}/4 - {x^ii}/4$ $b^2 = {3x^2}/four$ $b = {√3x}/2$ Then we're left with: $x/2, {x√3}/two, x$ At present permit's multiply each measure by 2, just to make life easier and avoid all the fractions. That way, we're left with: $x$, $x√3$, $2x$ We tin can see, therefore, that a 30-lx-xc triangle will always accept consistent side lengths of $ten$, $x√three$, and $2x$ (or $10/2$, ${√3x}/ii$, and $x$). Luckily for u.s., we tin prove 30-threescore-ninety triangle rules true without all of...this. Knowing the xxx-60-90 triangle rules will be able to salve you time and energy on a multitude of unlike math problems, namely a broad variety of geometry and trigonometry problems. Proper understanding of the 30-60-ninety triangles will allow you to solve geometry questions that would either be impossible to solve without knowing these ratio rules, or at the very least, would take considerable time and endeavour to solve the "long way." With the special triangle ratios, you can figure out missing triangle heights or leg lengths (without having to use the Pythagorean theorem), find the area of a triangle by using missing top or base of operations length information, and quickly calculate perimeters. Whatever fourth dimension you need speed to reply a question, remembering shortcuts like your thirty-60-ninety rules will come in handy. Memorizing and understanding the xxx-lx-90 triangle ratio volition also allow y'all to solve many trigonometry issues without either the demand for a calculator or the demand to guess your answers in decimal course. A 30-threescore-90 triangle has adequately elementary sines, cosines, and tangents for each angle (and these measurements volition always exist consistent). Sine of 30° volition always be $ane/2$. Cosine of lx° will always exist $one/2$. Though the other sines, cosines, and tangents are fairly simple, these are the two that are the easiest to memorize and are likely to show up on tests. So knowing these rules will let you to find these trigonometry measurements every bit rapidly equally possible. You know these xxx-60-90 ratio rules are useful, but how practice you lot go on the data in your head? Remembering the 30-60-ninety triangle rules is a affair of remembering the ratio of 1: √3 : 2, and knowing that the shortest side length is e'er opposite the shortest angle (xxx°) and the longest side length is always opposite the largest angle (90°). Some people memorize the ratio by thinking, "$\bi x$, $\bo two \bi x$, $\bi x \bo √ \bo3$," because the "1, 2, 3" succession is typically easy to remember. The 1 precaution to using this technique is to retrieve that the longest side is actually the $2x$, not the $x$ times $√3$. Another way to remember your ratios is to use a mnemonic wordplay on the 1: root 3: 2 ratio in their proper lodge. For case, "Jackie Mitchell struck out Lou Gehrig and 'won Ruthy too,'": one, root 3, two. (And information technology's a true baseball history fact to kick!) Play effectually with your ain mnemonic devices if these don't appeal to you—sing the ratio to a vocal, notice your ain "one, root 3, 2" phrases, or come up with a ratio poem. You lot can even just remember that a thirty-60-90 triangle is one-half an equilateral and figure out the measurements from at that place if yous don't like memorizing them. However it makes sense to you to remember these 30-60-90 rules, keep those ratios your caput for your future geometry and trigonometry questions. Memorization is your friend, yet you tin can make information technology happen. Does your school study your GPA as weighted or unweighted? What would your GPA exist, considered on a iv.0, 5.0, or half dozen.0 scale? Employ our tool to calculate your unweighted and weighted GPA to figure out how y'all stack upwards against other college applicants. Yous'll likewise get our proprietary higher cadre GPA calculation and communication on where to ameliorate to be a improve college applicant. Now that we've looked at the hows and whys of 30-threescore-ninety triangles, let's work through some do issues. A structure worker leans a 40-foot ladder up against the side of a building at an bending of 30 degrees off the ground. The ground is level and the side of the building is perpendicular to the ground. How far up the building does the ladder reach, to the nearest pes? Without knowing our xxx-lx-90 special triangle rules, we would have to use trigonometry and a figurer to detect the solution to this trouble, since we but have one side measurement of a triangle. But because we know that this is a special triangle, nosotros can find the answer in just seconds. If the building and the footing are perpendicular to one some other, that must hateful the edifice and the ground form a right (90°) bending. Information technology's also a given that the ladder meets the footing at a 30° angle. We tin can therefore come across that the remaining angle must be 60°, which makes this a thirty-60-90 triangle. Now we know that the hypotenuse (longest side) of this 30-60-90 is xl feet, which means that the shortest side will be half that length. (Remember that the longest side is always twice—$2x$—as long equally the shortest side.) Because the shortest side is opposite the 30° angle, and that angle is the caste measure of the ladder from the ground, that ways that the top of the ladder hits the building 20 anxiety off the ground. Our concluding answer is twenty feet. If, in a correct triangle, sin Θ = $ane/two$ and the shortest leg length is viii. What is the length of the missing side that is NOT the hypotenuse? Because you know your 30-60-90 rules, you tin solve this trouble without the need for either the pythagorean theorem or a calculator. Nosotros were told that this is a right triangle, and we know from our special right triangle rules that sine 30° = $1/2$. The missing angle must, therefore, be lx degrees, which makes this a 30-60-ninety triangle. And because this is a xxx-sixty-xc triangle, and nosotros were told that the shortest side is 8, the hypotenuse must be 16 and the missing side must be $8 * √3$, or $8√three$. Our terminal answer is 8√3. Remembering the rules for 30-threescore-90 triangles volition help y'all to shortcut your fashion through a multifariousness of math problems. Merely do keep in listen that, while knowing these rules is a handy tool to keep in your belt, you can notwithstanding solve most problems without them. Keep track of the rules of $10$, $ten√3$, $2x$ and thirty-60-xc in whatever way makes sense to you and attempt to continue them straight if you can, simply don't panic if your heed blanks out when it'due south crunch fourth dimension. Either fashion, you lot've got this. And, if you lot demand more practice, become ahead and check out this 30-lx-xc triangle quiz. Happy test-taking!
What Is a thirty-60-90 Triangle?
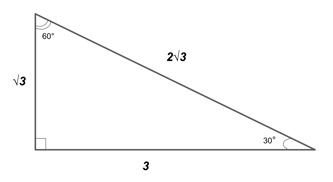
Example 1
Example ii
Example 3
Why It Works: xxx-60-90 Triangle Theorem Proof
When to Apply xxx-60-ninety Triangle Rules
Geometry
Trigonometry
Tips for Remembering the 30-60-90 Rules

Instance 30-60-90 Questions
Geometry
Trigonometry
The Take-Aways

About the Author
Courtney scored in the 99th percentile on the Sat in loftier school and went on to graduate from Stanford Academy with a degree in Cultural and Social Anthropology. She is passionate well-nigh bringing education and the tools to succeed to students from all backgrounds and walks of life, as she believes open up education is one of the swell societal equalizers. She has years of tutoring experience and writes creative works in her complimentary time.
Source: https://blog.prepscholar.com/30-60-90-triangle-ratio-formula#:~:text=And%20so%20on.,degree%20angle%20in%20this%20triangle.
0 Response to "How Do You Know Where the 60 Degree Angle Is in a Triangle"
Post a Comment